Spin update policies

In the Monte Carlo Metropolis algorithm new states of the system are generated from a previous state by randomly selecting a single spin and updating it to a new trial position (trial move). 𝕍egas supports eight possible trial moves: random, flip, qising, adaptive, cone30, cone15, hn30 and hn15.

• random

  This policy generates a random vector over a sphere of radius one and multiplies it by the spin norm. To generate a random vector, two random numbers ($u$ and $v$) in the range $\left( 0, 1 \right)$ are generated, then

  $\phi = 2\pi u$

  $\theta = \arccos \left( 2v - 1 \right)$

  and using spherical coordinates

  $S_x = \left|\mathbf{S}\right| \sin \left( \theta \right) \cos \left( \phi \right)$

  $S_y = \left|\mathbf{S}\right| \sin \left( \theta \right) \sin \left( \phi \right)$

  $S_z = \left|\mathbf{S}\right| \cos \left( \theta \right)$

  where $\left|S\right|$ is the spin norm. In this way, a random spin direction $\mathbf{S^{\prime}}$ with an uniform distribution $\mathbf{S^{\prime}} = S_x \hat{i} + S_y \hat{j} + S_z \hat{k}$ is generated.

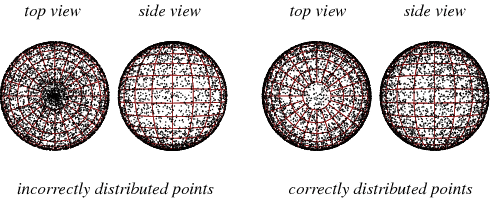
  Note that generating a random $\phi$ value in the range $\left[ 0, 2\pi \right)$ and a random $\theta$ value in the range $\left[ 0, \pi \right]$ is a incorrect way to generate a random vector, because the area element $dA = \sin\left(\theta\right)d\theta d\phi$ is a function of $\phi$. Therefore, the random vectors will tend to point to the poles.

  Wolfram Mathworld presents a good explanation of the generation of random points on the surface of a unit sphere, and shows some graphical schemes:

  

• flip

  This policy takes the initial spin direction ($\mathbf{S}$) and reverses it. The new spin direction will be $\mathbf{S^{\prime}} = -\mathbf{S}$. The spin directions are always pointing alog the $\hat{k}$ and $-\hat{k}$ axes. This trial move resembles the Ising model.

• qIsing

  Unlike the spin flip move, the qIsing move generates all possible projections of the spin moment. These projections are $-\left|\mathbf{S}\right|$, $-\left|\mathbf{S}\right| + 1$, $...$, $\left|\mathbf{S}\right| - 1$, $\left|\mathbf{S}\right|$. $\left|\mathbf{S}\right|$ must be multiple of $1/2$. Otherwise, the projections are not symmetric. Moreover, note that there are $2\left|\mathbf{S}\right| + 1$ possible projections. For example, if $\left|\mathbf{S}\right| = 3/2$, there are $4$ possible projections $\left(-3/2, -1/2, 1/2, 3/2\right)$, which is consistent with $4 = 2\times 3/2 + 1$. Like in the spin flip move, the spin directions are always pointing alog the $\hat{k}$ and $-\hat{k}$ axes.

• adaptive

  The Adaptive move generates the new spin direction ($\mathbf{S^{\prime}})$ in the vicinity of the initial spin direction ($\mathbf{S}$) employing a Gaussian distribution, according to the expression

  $\mathbf{S^{\prime}} = \left|\mathbf{S}\right| \frac{\frac{\mathbf{S}}{\left|\mathbf{S}\right|}+\sigma_{g}\mathbf{\Gamma}}{\left|\frac{\mathbf{S}}{\left|\mathbf{S}\right|}+\sigma_{g}\mathbf{\Gamma}\right|}$

  where $\mathbf{\Gamma}$ is a Gaussian distributed random vector and $\sigma_{g}$ is the width of the cone around the initial spin direction $\mathbf{S}$. The width of the cone is varied adaptively in order to keep an acceptance rate close to $50\%$, as follows: At each temperature, the simulation starts using a high cone width ($\sigma_{g}=60$) in the first Monte Carlo step. From then on, every MCS, the cone width is recalculated by multiplying the current cone width by a factor ($f$) obtained according to the acceptance rate ($R$) in the previous MCS

  $f=\frac{0.5}{1-R}\text{.}$

  The selection of the factor is made such that the cone width approaches values that generate an acceptance rate close to $50\%$. The Adaptive move is more efficient than other common spin update policies independently of the temperature and the anisotropy of the system in consideration.

• cone30 and cone15

  Also known as small step moves, the cone30 and cone15 moves generates new spin directions from a uniform probability distribution within a cone with a given opening angle around the initial spin direction, hence each spin can only move by small angular changes limited by the opening angle. The openin angle can be set to $30$º (cone30) or $15$º (cone15). These trial moves make use of the Rodrigues’ rotation formula.

• hn30 and hn15

  hn30 and hn15 are based on a trial move proposed by D. Hinzke and U. Nowak that performs a combined samplig. For each Monte Carlo step one trial move is randomly selected from a set of three random, one small step and one spin flip moves. Then, the selected trial move is applied to all the spin moments in that Monte Carlo step. hn30 and hn15 correspond to trial moves where the set is composed by a cone30 and cone15 moves, respectively.

• Home

• Model and method

• Installation

• System building

• Simulation and data analysis

• Tutorials